PureWhiteVK's Blog

发表于 分类于 本文字数： 1k 阅读时长 ≈ 4 分钟

Grid 绘制方式

之前一直想知道各种三维软件中虚拟网格是怎么绘制的，就上网搜了一下相关实现，没想到里面小细节还挺多的，就用一篇博客记录一下吧 ( •̀ ω •́ )。

下图展示了 blender 中网格的效果：

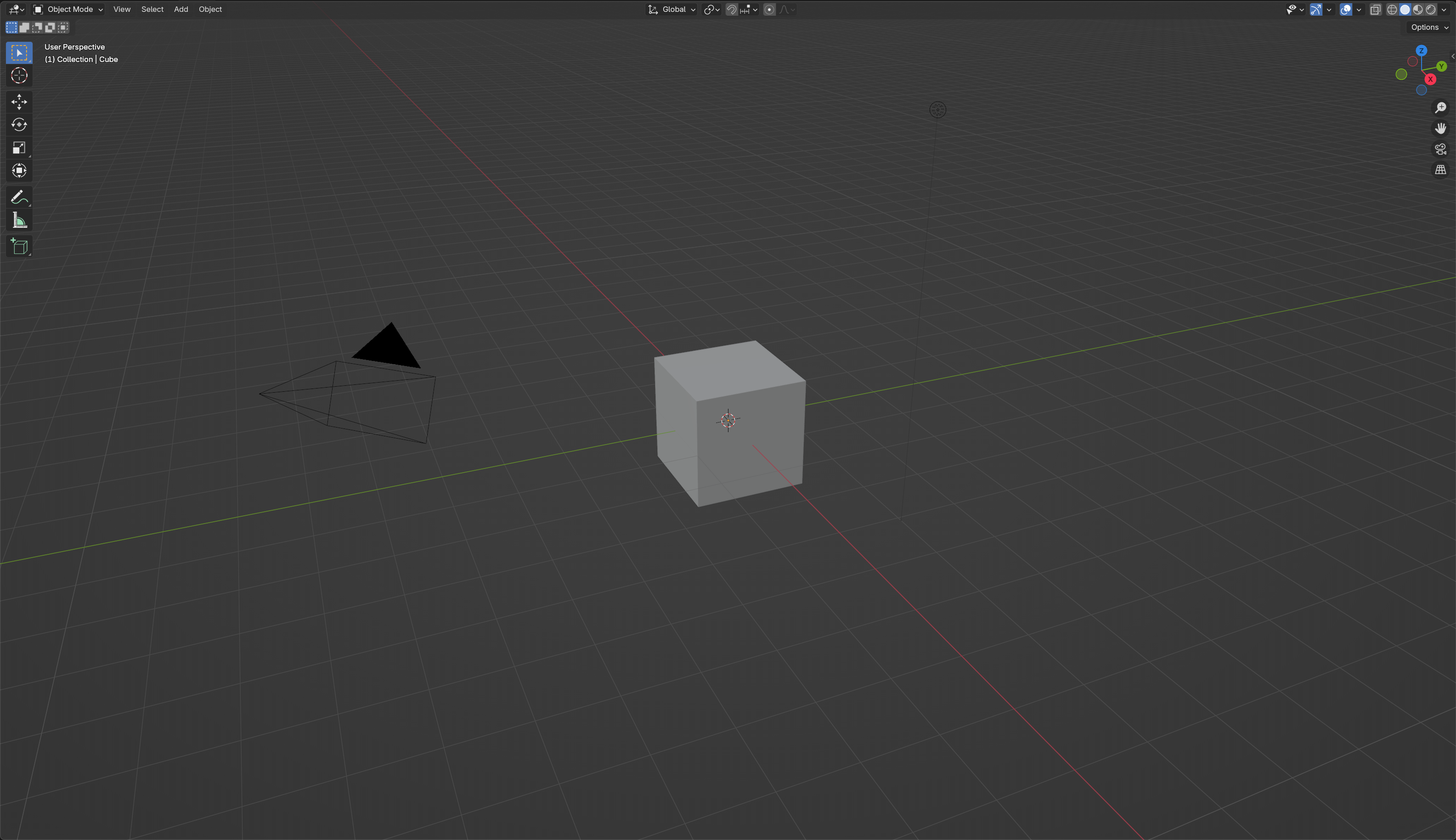
从图中可以看到几个基本特征：

  1. 网格绘制在世界坐标系下的底面（在一般的右手系坐标系中，Z轴向上，X轴向前，Y轴向右），则对应 XY 平面；

  2. x 轴标记为红色 \((1,0,0)\)，y轴标记为 \((0,1,0)\)

  3. 按照固定间隔绘制网格

阅读全文 »

发表于 分类于 本文字数： 474 阅读时长 ≈ 2 分钟

最近需要在离线开发环境中配置 VS Code 环境，本来是想在 Web 网页上手动下载，然后在 VS Code 下使用的，结果发现有些插件是没法直接下载打包好的插件的（.vsix）文件，搜索了一下，发现可以直接在 VS Code 插件面板里下载，就记录一下如何下载的。

准备安装包

首先在外网机中准备好 VS Code 和对应版本的安装包（一般直接使用最新版即可），通过下列方式查询 VS Code 版本

可以在 这里 下载到对应的安装包。

Caution

一定要确保安装包和外网机安装的 VSCode 版本一致，否则下载的插件可能无法正常安装！

阅读全文 »

发表于 分类于 本文字数： 1.4k 阅读时长 ≈ 5 分钟

Hello, Shader Toy

Shader（着色器）简单来说就是运行在 GPU 上的一小段程序，用来控制图形渲染的方式。

在传统渲染管线中，GPU 会自动执行一套固定流程，但 shader 的出现让开发者能够自定义这些流程，从而实现更灵活和更复杂的图形效果。

Shader Toy 是一个在线的 Shader 变成和展示网站，可以展示实时的 Shader 编程效果。

在图形 API （OpenGL）中，支持多种 Shader 类型：

  • Vertex Shader（顶点着色器）
  • Tessellation Shader（细分着色器）
  • Geometry Shader（几何着色器）
  • Fragment Shader（片段着色器）
  • Compute Shader（计算着色器）

而在 Shader Toy 中的 Shader 特指 Fragment Shader，其输入的是一个覆盖整个显示区域的四边形，可以在 Fragment Shader 中决定显示区域中每一个像素的颜色（rgba）。

阅读全文 »

发表于 分类于 本文字数： 2.5k 阅读时长 ≈ 9 分钟

Hello Projection

所谓投影，就是 将高维空间中的对象，通过某种方式映射到低维或另外一个空间中。如下图所示（图片来自网络）。

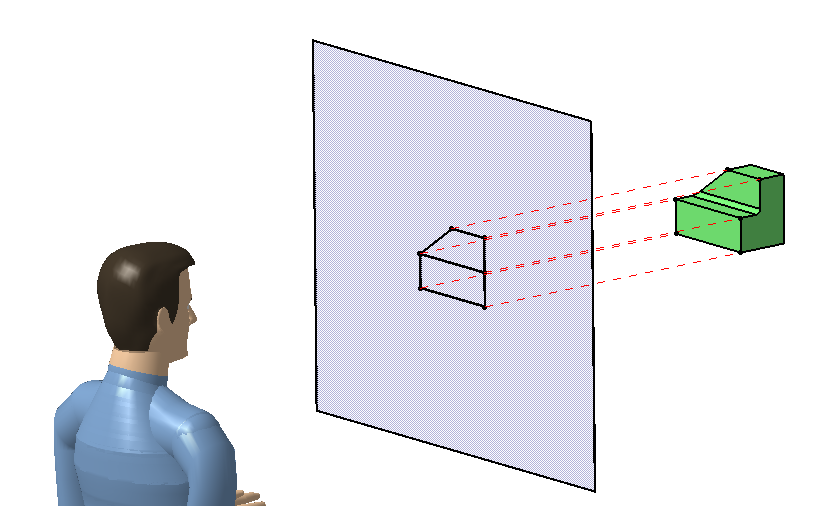
当在二维平面上展示三维物体时，其展示的是三维物体在二维空间上的一个投影，而这个三维到二维的转换过程就是投影变换。

如果投影过程是一个线性变换，则可以通过一个矩阵描述变换，如下式所示，其中 \(M_\text{projection}\) 就称为投影变换矩阵。 \[ P^{\prime} = M_{\text{projection}} \cdot P \]

阅读全文 »

发表于 分类于 本文字数： 2.1k 阅读时长 ≈ 8 分钟

最近写博客时，发现 github markdown 中提供的 Alerts 很有用，能够作为提示信息进行展示。

其实际上是在 引用文本（Quoting text） 的基础上添加了一个特殊的 tag，使其渲染时有特殊的显示效果，markdown 代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
> [!NOTE]
> Useful information that users should know, even when skimming content.

> [!TIP]
> Helpful advice for doing things better or more easily.

> [!IMPORTANT]
> Key information users need to know to achieve their goal.

> [!WARNING]
> Urgent info that needs immediate user attention to avoid problems.

> [!CAUTION]
> Advises about risks or negative outcomes of certain actions.

渲染结果如下：

本来以为这是 gfm（GitHub Flavored Markdown Spec）规范的一部分，但是发现这个功能是 Github 单独实现的一个功能，hexo 上默认是不支持的，不过搜了一下似乎实现起来并不复杂，就用一篇博客记录下如何实现的。

阅读全文 »

发表于 分类于 本文字数： 3.6k 阅读时长 ≈ 13 分钟

Conan 作为一个 C++ 包管理工具，相对于之前介绍的 CMake FetchContent 或者 ExternalProject 方式添加第三方依赖会更加简单，但是凡是碰上了 C++，都简单不到哪去，学习成本还是有一点的，就用一篇笔记介绍一下 Conan 的基本使用。

安装 Conan

由于我们后面会大量使用 conanfile.py，且也可以借助 Python 插件实现 conanfile.py 的代码补全，直接使用 python 库的方式安装 conan，安装命令如下：

1
python -m pip install conan

安装之后例行检查一下版本

1
conan --version

阅读全文 »

发表于 分类于 本文字数： 546 阅读时长 ≈ 2 分钟

Powershell 设置

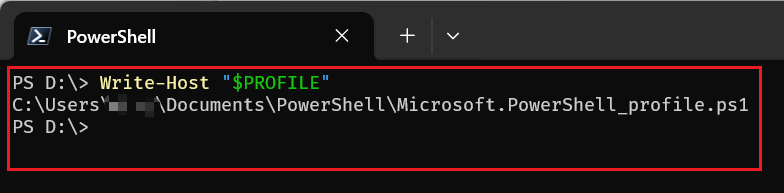
通过 $PROFILE 变量，可以查询到 Powershell 默认加载的配置文件路径，如下所示

如果文件不存在，直接创建一个即可，然后填入下面两个预定义的函数（默认代理的地址为 127.0.0.1:7890，纪念天国的CFW🙏）

1
2
3
4
5
6
7
8
9
10
11
12
function proxy_on {
    $proxy="http://127.0.0.1:7890"
    $Env:http_proxy = "$proxy"
    $Env:https_proxy = "$proxy"
    Write-Host "Proxy enabled: $proxy"
}

function proxy_off {
    Remove-Item Env:\http_proxy -ErrorAction SilentlyContinue
    Remove-Item Env:\https_proxy -ErrorAction SilentlyContinue
    Write-Host "Proxy disabled"
}

当更改完 $PROFILE 文件后，使用 . $PROFILE 加载更新后的配置文件，并通过简单的 curl 命令判断是否可用

阅读全文 »

发表于 分类于 本文字数： 2.4k 阅读时长 ≈ 9 分钟

git clone

1
git clone <repo-url>

示例命令如下

1
git clone https://github.com/boostorg/boost.git

一些常用的参数（全部参数选项可以通过 git clone --help 查看）

  • --recursive 或 --recurse-submodules（在较新版本的 git 中使用，命令的语义更加清晰）：当要拉取的仓库中包含 submodule 时，是默认不会拉取子仓库的，而指定这个参数即可拉取所有的子仓库。

    如果我们在下载的时候忘记指定 --recursive，也可以通过下面命令重新拉取子仓库

    1
    git submodule update --init --recursive

  • --depth：当我们只想下载指定更新次数的分支（这样可以减少下载的大小，在我们只需要最新的提交记录时很有用，当然也可以直接下载 zip 或 tar.gz 等压缩文件来解决。

  • -b 或者 --branch：指定要拉取的分支名称，例如下载 boost-1.86.0 （这个实际上是一个 tag，但也可以通过这种方式下载）。

    1
    git clone https://github.com/boostorg/boost.git --branch boost-1.86.0
阅读全文 »

发表于 分类于 本文字数： 1.3k 阅读时长 ≈ 5 分钟

对于一个\(2^n\times2^n\)的二维网格由于地址空间都是一维的（例如0x0000到0xffff），其实际在计算机中会将多维压缩成一维，可以形式化表示为

\[ \begin{align} M_{\text{2D}}&:(x,y)\to v \\ M_{\text{2D}}^{-1}&:v\to (x,y) \\ \end{align} \]

对于\(M_{\text{2D}}(x,y)\)也可记作\(\text{encode}(x,y)\)，\(M^{-1}_{\text{2D}}(v)\)为\(decode(v)\)

Linear Curve

一种最为简单的存储方式就是逐行地或逐列地存储二维数据，对于一个指定大小的二维方块（\(w\times h\)），从0开始的坐标\((x,y)\) 对应的一维地址为（一行包含\(w\)个元素） \[ v = x \times w + y \] 同理，将一维坐标\((v)\)转换二维方块坐标也很简单，只需要对行/列进行整除和取余操作即可 \[ \begin{align} x &= \lfloor v / w \rfloor \\ y &= v - x \times w \end{align} \] 上面这种方式在一般情况下足够使用，但是对于纹理/体素等数据的读取时，通常会利用到二维/三维坐标的局部性（即当我们访问坐标\((x,y)\)时，我们有很大概率将访问该坐标周围的坐标），而使用线性存储方式则会丢失这种局部性。

例如对于一个\(16 \times 16\)的方块中坐标\((4,4)\)和坐标\((6,6)\)，其二维曼哈顿距离为 \[ (6-4)+(6-4) = 4 \] 而经过线性存储映射后距离为 \[ (6*16+6)-(4*16+4)=38 \] ，可以观察到经过一维映射后两个数据距离相差较远。

下图展示了 linear curve 的示意图

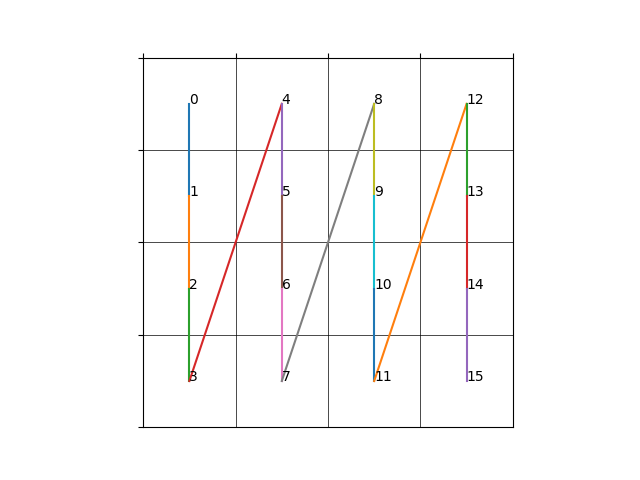
直接说距离似乎难以理解这种差距，考虑一个实际读取场景，假设CPU的cache一次可以存放16个数据，当我们读取纹理中\((4,4)\)位置的数据后，下一个准备读取其周围\((6,6)\)的数据，由于\((6,6)\)的数据在内存中地址距离\((4,4)\)数据地址较远，无法一次加载到cache中，即出现cache miss，这样我们就只能从内存中重新加载数据，无法利用高速缓存，影响数据读取性能。

针对这个问题，可以使用Hilbert曲线或者Morton曲线这类特殊的映射方式进行坐标映射

阅读全文 »
0%