绘制 grid

发表于 2025/10/12 分类于计算机图形学本文字数： 6.1k 阅读时长 ≈ 22 分钟

之前一直想知道各种三维软件中虚拟网格是怎么绘制的，就上网搜了一下相关实现，没想到里面小细节还挺多的，就用一篇博客记录一下吧 ( •̀ ω •́ )。

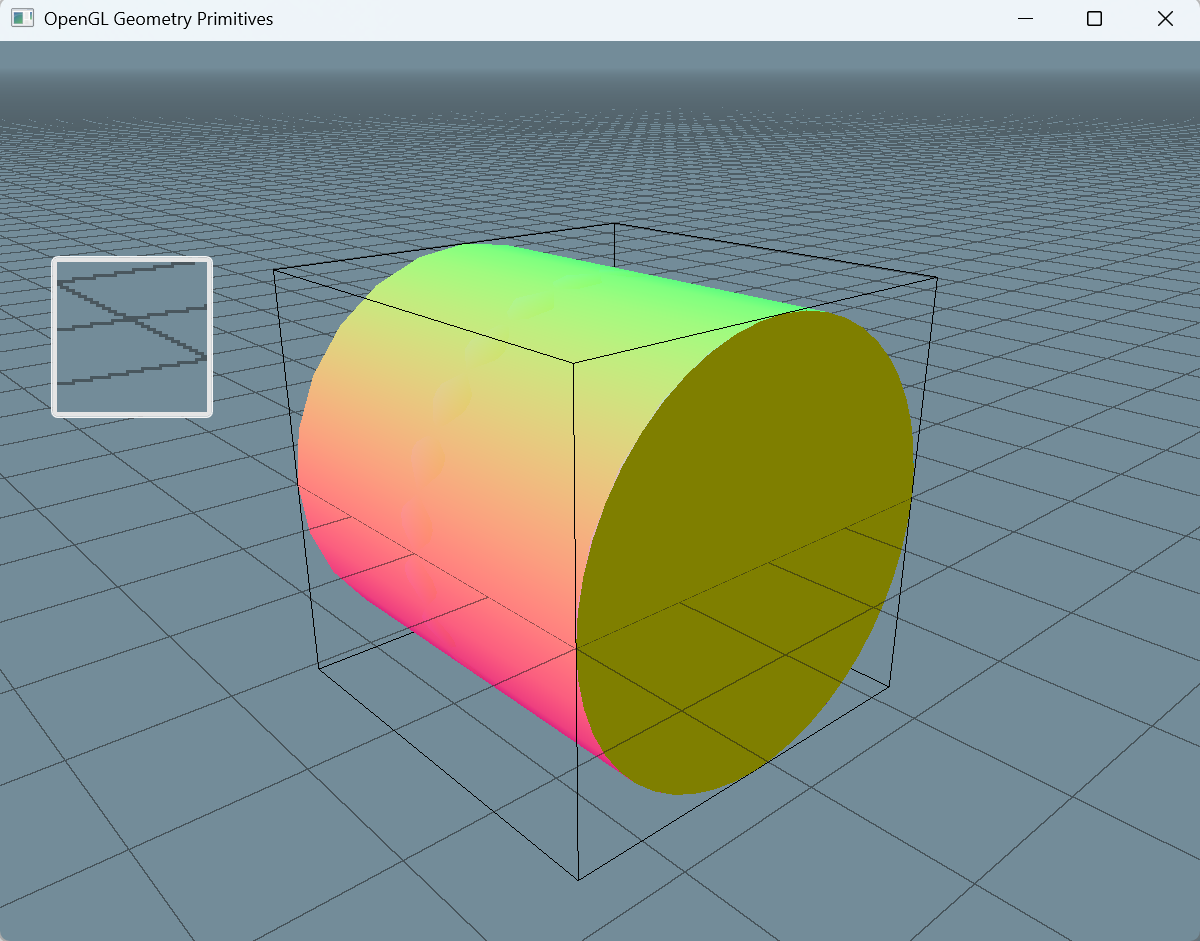
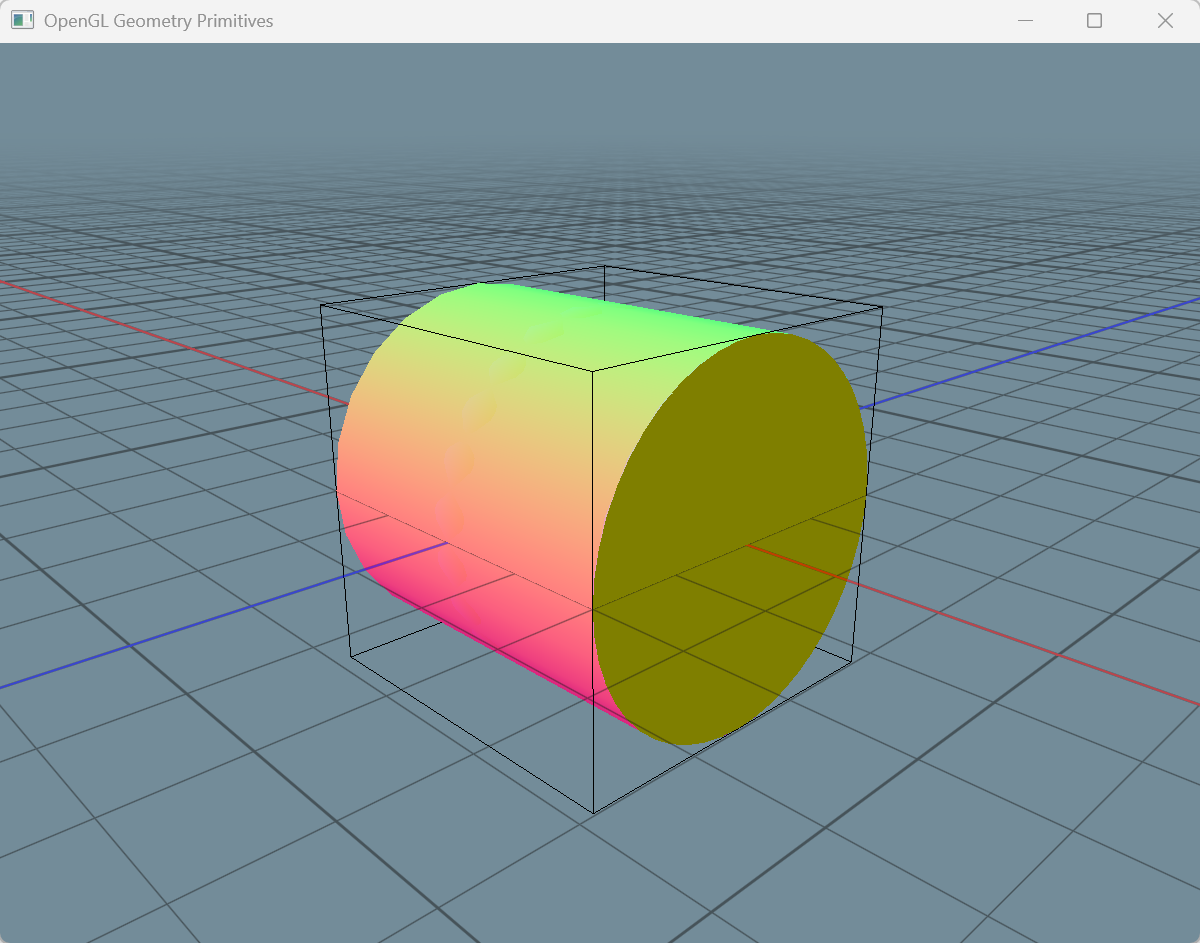
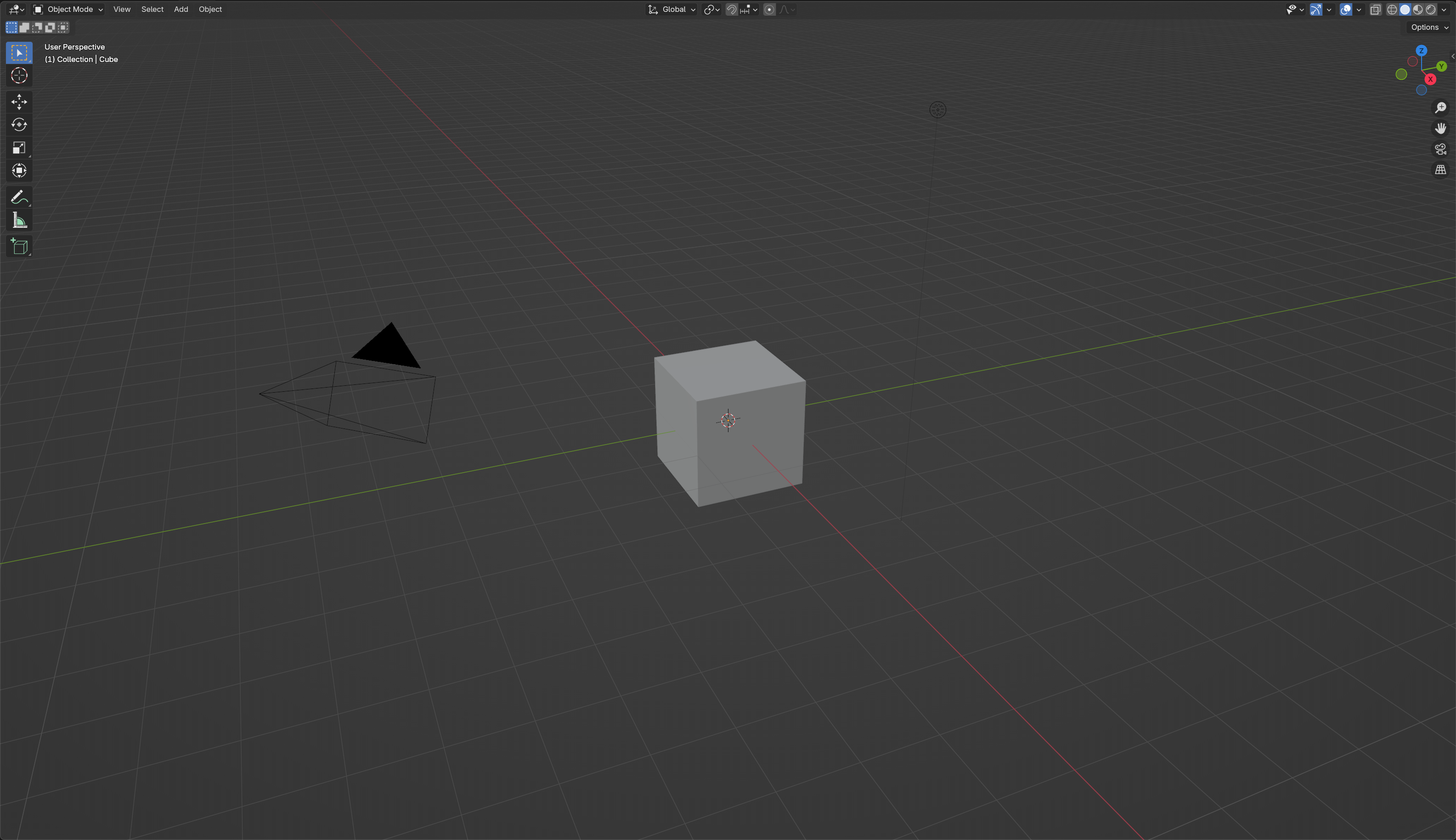
下图展示了 blender 中网格的效果：

从图中可以看到几个基本特征：

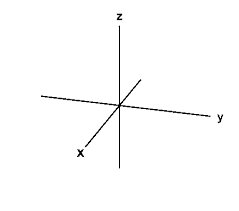
网格绘制在世界坐标系下的底面（在一般的右手系坐标系中，Z轴向上，X轴向前，Y轴向右），则对应 XY 平面；
x 轴标记为红色 $(1,0,0)$，y轴标记为绿色 $(0,1,0)$
按照固定间隔绘制网格

$\require{physics}$

绘制二维网格

在世界坐标系下添加一个超级大的三维实体平面（例如 100x100 的平面），再通过网格图样生成平面的 texture，完成网格的绘制
在屏幕空间中绘制虚拟平面，在虚拟平面上绘制网格图样。

其实第一种和第二种的思路都差不多，关键在于找到网格所在平面，并在平面上绘制网格样式。

两种方式最终都会回到网格图样的绘制，那么我们先考虑如何在二维平面上绘制网格。在二维平面上绘制东西，这不是又回到了之前介绍的 Shader Toy 吗，在那篇文章中也通过 Shader Toy 展示了二维网格的绘制效果，但并没有介绍其绘制的原理，这次就详细介绍一下具体是如何绘制的。

绘制直线

网格是由一条一条平行于坐标轴的直线构成的，每条直线的函数都类似于 $y=1$ 和 $x=2$ 这种。但要在二维空间中绘制 $x=1$ 这条直线，除了函数定义外，还需要指定直线的宽度，例如宽度为 1个像素、2个像素，又或者是相对于屏幕宽度的百分比（例如 $0.1\%$）等。

设直线的宽度为 $w$，我们要绘制的实际上是由 $x=1-{w}/{2}$ 和 $x=1+w/2$ 两条直线所围成的区域，即满足如下分段函数形式： \[ L(x) = \begin{cases} 1, & 1-\frac{w}{2} \le x \le 1 + \frac{w}{2} \\[4pt] 0, & \text{else} \end{cases} \] 而在绘制直线时，只需要根据 $w(x)$ 的函数值进行绘制即可，值为 1 时绘制直线，值为0 时不绘制。

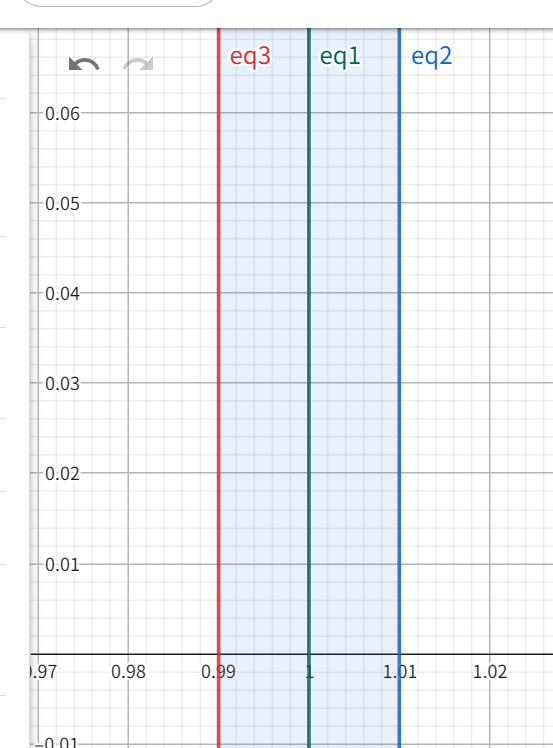
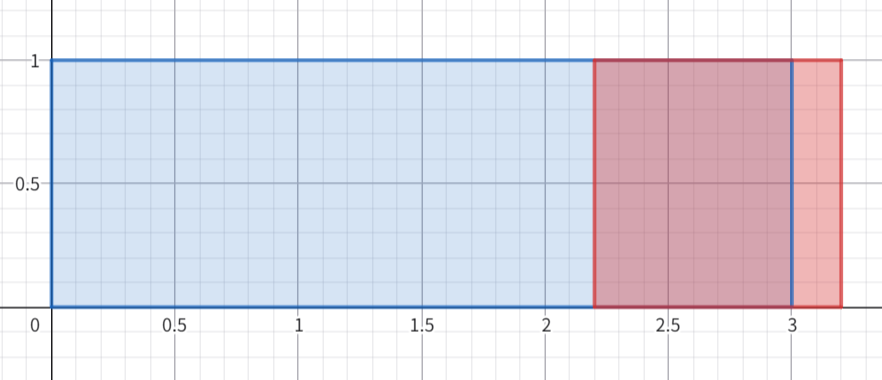
对于 $x=1,w=0.02$，直线的可视化效果如下：

其中 eq1（中间绿色直线）为目标直线 $x=1$，eq2（右边蓝色直线） $x=0.99$ 和 eq3（左边红色直线） $x=1.01$ 为实际用于判断的边界直线。

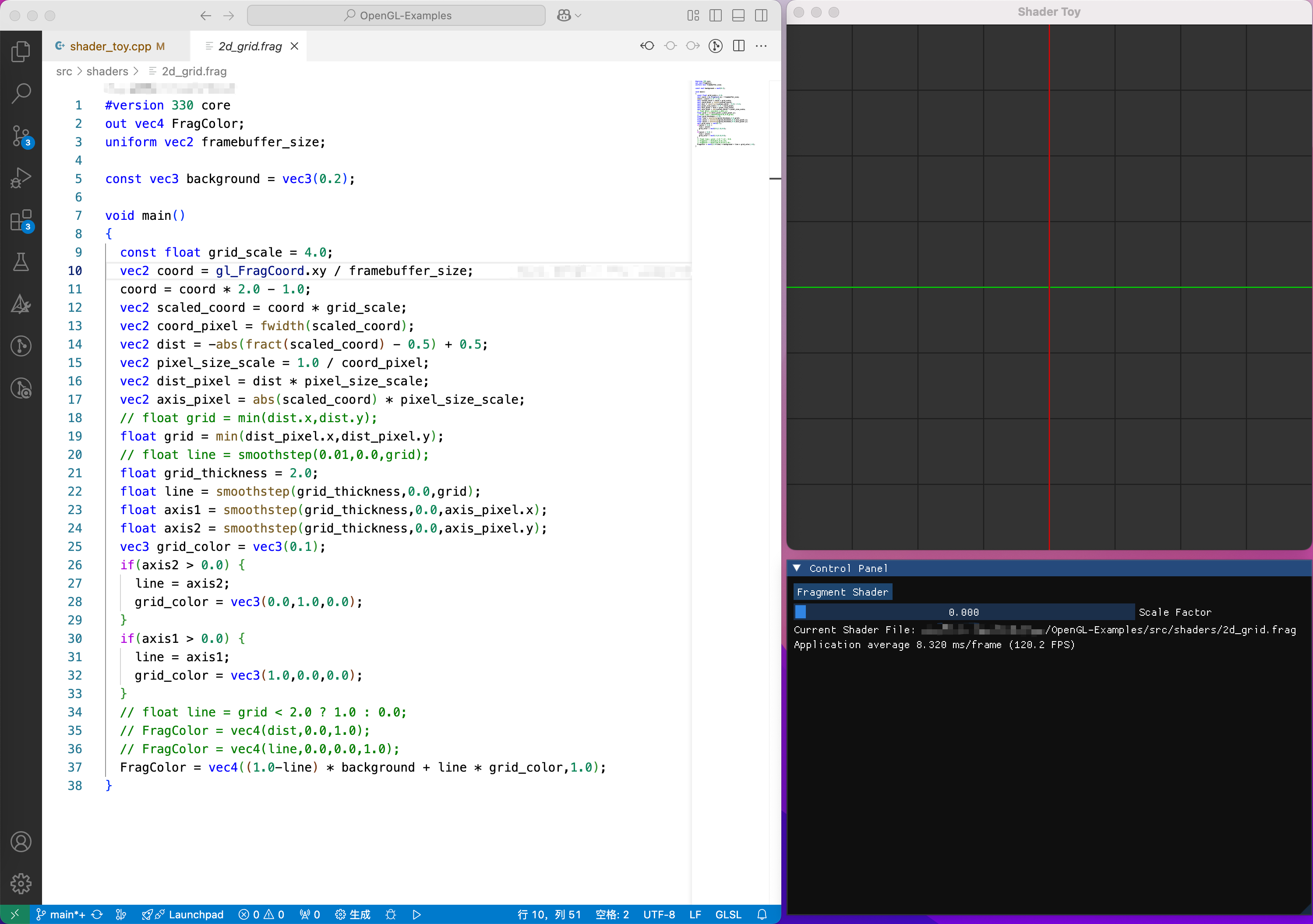
对应到 fragment shader 中，直接根据 $w(x)$ 函数进行绘制即可，代码如下：

2d_line.frag

#version 330 core
out vec4 FragColor;
uniform vec2 framebuffer_size;

void main()
{
  vec2 coord = gl_FragCoord.xy / framebuffer_size;
  float target_coord = 0.5;
  float line_width = 0.01;
  float draw_line = float(coord.x >= target_coord - line_width * 0.5 && coord.x <= target_coord + line_width * 0.5);
  FragColor = vec4(draw_line,0.0,0.0,1.0);
}

其在 $x=0.5$ 处绘制了一条宽度为 $0.01$ 的直线，此处宽度是相对于屏幕宽度而言的（其实际像素宽度为 $\text{width} * 0.01$），在不同的 framebuffer 大小下，直线的宽度会随之发生变化。

如果需要将其宽度指定为像素宽度，只需要在计算前将 line_width 的单位从百分比切换成像素宽度即可，如下所示：

2d_line_fixed_width.frag

#version 330 core
out vec4 FragColor;
uniform vec2 framebuffer_size;

void main()
{
  vec2 coord = gl_FragCoord.xy / framebuffer_size;
  float target_coord = 0.5;
  float line_width = 1 / framebuffer_size.x;
  float draw_line = float(coord.x >= target_coord - line_width * 0.5 && coord.x <= target_coord + line_width * 0.5);
  FragColor = vec4(draw_line,0.0,0.0,1.0);
}

其中 1 / framebuffer_size.x 表示直线宽度为 1 个像素时，对应屏幕百分比宽度是多少，这样就可以确保直线的宽度不随 frame buffer 大小改变了。

绘制网格

网格的绘制实际上就是在 x 轴方向和 y 轴方向按照重复绘制多次直线即可，有两种方式可以实现重复绘制。

第一种就是通过 for 循环方式，手动展开绘制，如下所示：

for X in [ 0.1,0.3,0.5,0.7,0.9 ]:
	draw_line x=X
for Y in [ 0.1,0.3,0.5,0.7,0.9 ]:
	draw_line y=Y

这种方式通过两个 for 循环，在 x 轴方向和 y 轴方向分别绘制 5 条直线，实现 grid 效果，对应的 shader 和渲染结果如下：

2d_grid_for_loop.frag

#version 330 core
out vec4 FragColor;
uniform vec2 framebuffer_size;

float draw_x_line(vec2 coord,float x,float line_width) {
  return float(coord.x >= x - line_width * 0.5 && coord.x <= x + line_width * 0.5);
}

float draw_y_line(vec2 coord,float y,float line_width) {
  return float(coord.y >= y - line_width * 0.5 && coord.y <= y + line_width * 0.5);
}

void main()
{
  vec2 coord = gl_FragCoord.xy / framebuffer_size;
  float line_width = 4 / framebuffer_size.x;
  float draw = 0.0;
  draw += draw_x_line(coord,0.1,line_width);
  draw += draw_x_line(coord,0.3,line_width);
  draw += draw_x_line(coord,0.5,line_width);
  draw += draw_x_line(coord,0.7,line_width);
  draw += draw_x_line(coord,0.9,line_width);

  draw += draw_y_line(coord,0.1,line_width);
  draw += draw_y_line(coord,0.3,line_width);
  draw += draw_y_line(coord,0.5,line_width);
  draw += draw_y_line(coord,0.7,line_width);
  draw += draw_y_line(coord,0.9,line_width);

  
  FragColor = vec4(clamp(draw,0.0,1.0),0.0,0.0,1.0);
}

渲染结果如下

这种方式通过硬编码方式指定网格的分辨率，但写起来很臃肿，有没有其他办法呢？

当然是有的，我们假设网格的宽度固定为 $s = 0.1$（也就是两条 grid line 之间距离为 10% 屏幕宽度），可以将 x 轴（$[-0.05,1.05]$）划分成 11 个区间，每个区间宽度为 0.1，具体如下所示：

[-0.05,0.05] ,  [0.05,0,15] , [0.15,0.25],
[ 0.25,0.35] ,  [0.35,0.45] , [0.45,0.55],
[ 0.55,0.65] ,  [0.65,0.75] , [0.75,0.85],
[ 0.85,0.95] ,  [0.95,1.05]

可以推导处每个区间的左边界和右边界公式如下： \[ [(k-0.5) \cdot s ,(k+0.5) \cdot s] , k \in \mathcal{Z} \] 而我们需要绘制的就是区间中心 $x = k \cdot s$ 或者 $y = k\cdot s$，直线的绘制区间如下所示（ $t$ 表示 $x$ 或者 $y$，$w$ 表示直线宽度）： \[ k \cdot s - w \cdot 0.5 < t < k \cdot s + w \cdot 0.5 \]

Tip

此时绘制的 grid 会将 $[0,1]$ 均分为 $1/s$ 份，直线坐标为 $[0,1/s,2/s,\cdots]$ 。

如果需要绘制经过 $(0.5,0.5)$ 的 grid，只需要将 $(x,y)$ 偏移 0.5 即可，即 $x^{\prime} = x + 0.5, y^{\prime}=y+0.5$。

此时如果想要判断一个 fragment 坐标 $(x,y)$（已经缩放到 $[0,1]^2$ ）是否应该绘制，即判断该 fragment 是否在任意一条直线的绘制区间内，可以对上述绘制区间进行一些变换，如下所示： \[ \begin{align} &k \cdot s - w \cdot 0.5 < t < k \cdot s + w \cdot 0.5 \\ \Rightarrow \; & - w \cdot 0.5 < t - k \cdot s < w \cdot 0.5 \\ \Rightarrow \; & \left| t - k \cdot s \right| < w \cdot 0.5 \end{align} \]

下一步就是找到 t 和 k 的关系，得到仅关于 t 的不等式，还是通过上述例子进行分析，通过归纳法不难得到 t 和 k 之间可以使用 floor 操作进行转换：

当 k = 0  时，t 位于 -0.05 到 0.05 间，中心为 0.0
当 k = 1  时，t 位于  0.05 到 0.15 间，中心为 0.1
当 k = 2  时，t 位于  0.15 到 0.25 间，中心为 0.2
当 k = 3  时，t 位于  0.25 到 0.35 间，中心为 0.3
...
当 k = 10 时，t 位于  0.95 到 1.05 间，中心为 1.0

$t$ 的取值范围为 $[0,1]$，$k$ 的取值范围为 $[0,1,\cdots,10]$，可以得到： \[ k = \left\lfloor \frac{t}{0.1} + 0.5\right\rfloor \] 其中 $\lfloor x \rfloor$ 表示向下取整操作，例如 $\lfloor0.1\rfloor=0$，$\lfloor2.1\rfloor=2$，对于任意指定的网格宽度，可总结 $k$ 和 $t$ 的关系如下所示： \[ k = \left\lfloor\frac{t}{s} + 0.5\right\rfloor \] 将 $k$ 和 $t$ 的关系带入上面的不等式，可以得到最终的判断不等式，令 $s^{\prime}=1/s $ ，有： \[ \left| t \cdot s^\prime - \left\lfloor t \cdot {s^\prime} + 0.5\right\rfloor \right| < w \cdot s^\prime \] 最终在 2d 平面上的 shader 如下所示：

2d_grid.frag

#version 330 core
out vec4 FragColor;
uniform vec2 framebuffer_size;

void main()
{
  vec2 inv_scale = 1.0 / framebuffer_size;
  vec2 coord = gl_FragCoord.xy * inv_scale;
  float line_width = 2.0 * inv_scale.x;
  float draw = 0.0;
  vec2 grid_scale = vec2(20,20);
  vec2 range = line_width * grid_scale * 0.5;
  vec2 scaled_coord = (coord + 0.5) * grid_scale;
  vec2 coord_new = abs(scaled_coord - floor(scaled_coord + 0.5));
  draw = float(
    (abs(coord_new.x) < range.x) || 
    (abs(coord_new.y) < range.y)
  );
  FragColor = vec4(draw,0.0,0.0,1.0);
}

下图展示了 shader 的绘制效果

回到三维

在三维空间中，只需要准备一个三维平面，然后使用 uv 坐标即可绘制。这里三维平面可以在 shader 中生成，也可以使用一个长方形的 mesh 进行绘制。

绘制三维平面

绘制 mesh 的方式实现很简单，但是需要一直调整 mesh 的大小，确保其在视野范围内一直可见，那么有没有什么更好的方式呢？

当然也是有的，这种绘制方式称为 infinite grid，只需要一个 DrawCall 就可以绘制一个无限大（看起来）的网格。

其绘制过程包含4步：

绘制一个覆盖全屏幕的长方形
对于屏幕空间上每一个像素点，构造一条从近平面经过该像素射向远平面的射线，并将其逆变换到世界坐标系下
判断射线是否和世界坐标系下某个平面相交（例如 xz 平面）
如果射线和平面相交，计算交点处的坐标和纹理坐标，通过二维网格绘制方法绘制网格

对于第1步和第4步，我们都已经知道怎么做了，这里主要详细说明如何进行坐标的逆变换和射线与平面求交。

对于世界坐标系下一点，在指定观察视角下，通过透视投影绘制到屏幕空间中，其会经过两个变换，视角变换（View transform）和投影变换（Projection transform），如下所示： \[ p_{\text{NDC}} = P \cdot V \cdot p_{\text{world}} \] 如果已知 NDC 下一个点，可以通过矩阵的逆求出该点在世界坐标系下的坐标： \[ p_{\text{world}} = V^{-1}\cdot P^{-1} \cdot p_{\text{NDC}} \] 设屏幕（NDC）上一点坐标为 $(x,y)$，其在近平面点坐标为 $p_0=(x,y,-1,1)$，在远平面点坐标为 $p_1=(x,y,1,1)$，经过逆变换可得两点世界坐标为 $p^{\prime}_0=(x_0^\prime,y_0^\prime,z_0^\prime)$ 和 $p^{\prime}_1=(x^\prime_1,y^\prime_1,z^\prime_1)$。此时可得直线参数方程如下： \[ l(t) = p^{\prime}_0 + t \cdot (p^{\prime}_{1} - p^{\prime}_{0}) \] 对于平面而言，其定义为： \[ n \cdot (p-d) = 0 \] 其中 $n$ 表示平面的法向量，$d$ 表示平面上一点，$p$ 表示世界坐标系上任意一点

将直线的参数方程带入平面方程，可求出交点的参数 t： \[ \begin{align} n \cdot (p^{\prime}_0 + t & \cdot (p^{\prime}_{1} - p^{\prime}_{0})-d) = 0 \\ t& = \frac{d - n\cdot p^{\prime}_0}{p^{\prime}_{1} - p^{\prime}_{0}} \end{align} \] 以平面 XoZ 为例，其法向量为 $(0,1,0)$ 且过原点 $(0,0,0)$，带入公式，可交点 $p_{\text{i}}$ 的参数$t_i$： \[ t = - \frac{y^{\prime}_0}{y^{\prime}_1 - y^\prime_0} = \frac{y^{\prime}_0}{y^{\prime}_0 - y^\prime_1} \\ \] 这样我们就算出了射线和平面的交点，之后直接使用世界坐标进行绘制即可（以 XoZ 平面为例，将交点处的 xz 坐标作为 uv 值，按照一定缩放比例使用前面提到的二维网格绘制方式进行绘制）。

下面给出第一版三维 grid 的完整代码

3d-grid-v1.vert

#version 330 core
uniform mat4 inv_view_proj;
// one giant triangle that covers the screen
const vec2 gridPlane[3] = vec2[3](
  vec2(-1.0,-1.0),
  vec2( 3.0,-1.0),
  vec2(-1.0, 3.0)
);
out vec3 near_point;
out vec3 far_point;
void main() {
    vec2 p = gridPlane[gl_VertexID];
    // near point in ndc coordinate
    vec4 point = inv_view_proj * vec4(p,-1.0,1.0);
    near_point = point.xyz / point.w;
    // far point in ndc corrdinate
    point = inv_view_proj * vec4(p,1.0,1.0);
    far_point = point.xyz / point.w;
    gl_Position = vec4(p,0.0, 1.0); // using directly the clipped coordinates
}

3d-grid-v1.frag

#version 330 core
in vec3 near_point;
in vec3 far_point;
out vec4 out_color;

uniform mat4 proj_view;
uniform float near;
uniform float far;

uniform vec3 grid_color = vec3(0.1,0.1,0.1);
uniform float grid_size = 0.5;
uniform float grid_thickness = 1.5;

vec4 draw_grid(vec3 world_pos, float grid_size, float grid_thickness, bool draw_axis){
  vec2 grid_coord = world_pos.xz / grid_size;
  vec2 grid_dist_world = abs(grid_coord - floor(grid_coord + 0.5));
  float draw = float( 
    (abs(grid_dist_world.x) < grid_thickness) ||
    (abs(grid_dist_world.y) < grid_thickness)
  );
  return vec4(grid_color,draw);
}

void main() {
    float t = -near_point.y / (far_point.y - near_point.y);
    vec3 world_pos = near_point + t * (far_point - near_point);
    float draw_plane = float(t>0.0);
    vec4 color = draw_grid(world_pos,grid_size,grid_thickness,true);
    out_color = vec4(color.xyz,draw_plane * color.w);
}

cpp 绘制部分，只需要准备 shader 对应的 uniform 变量即可，如下所示：

if (draw_grid) {
  glm::mat4 proj_view = projection * view;
  glm::mat4 inv_view_proj = glm::inverse(proj_view);
  grid_shader.use();
  grid_shader.set_uniform("proj_view", proj_view);
  grid_shader.set_uniform("inv_view_proj", inv_view_proj);
  grid_shader.set_uniform("near", near);
  grid_shader.set_uniform("far", far);
  grid_shader.set_uniform("set_depth", static_cast<float>(set_depth));
  grid_shader.set_uniform("grid_size", grid_size);
  grid_shader.set_uniform("grid_thickness", grid_thickness1);
  glBindVertexArray(dummy_vao);
  glDrawArrays(GL_TRIANGLES, 0, 3);
}

由于我们在 vertex shader 中使用了一个覆盖整块屏幕的大三角形，这里就只需要一个 Draw Call 就可以完成网格的绘制。

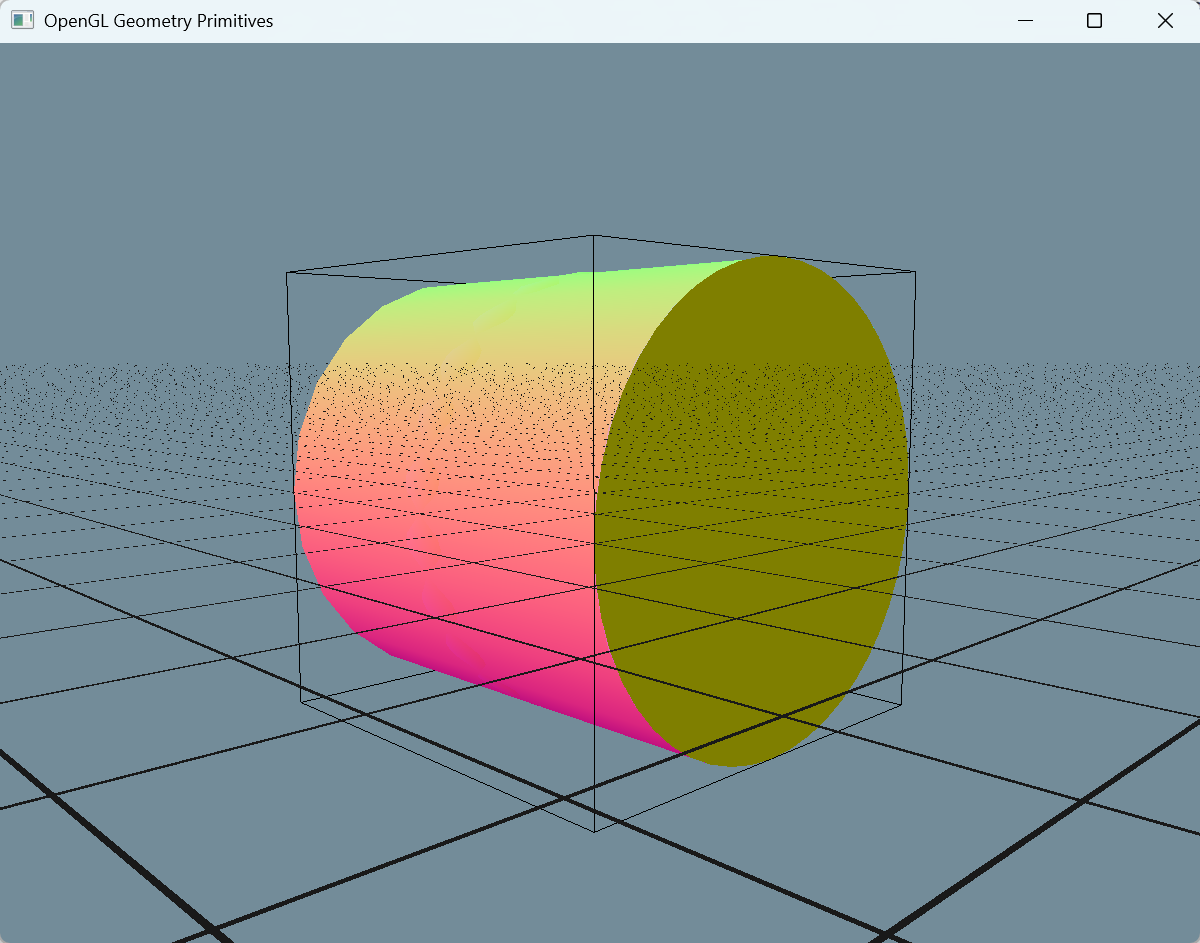
最终效果如下图所示（固定 grid_size 为 0.5，grid_thickness 为 0.01）：

从图中可以看到几个需要改善的点：

线宽不统一，似乎是靠近相机的更粗，而远方的几乎看不见
没有正确处理深度关系，立体感不强

固定线宽

从二维网格的绘制原理可以知道，其关键在于下面这个公式： \[ \left| c - \left\lfloor c + 0.5\right\rfloor \right| < d \] 其中 $c$ 为某个二维坐标，而 $d$ 为网格的线宽。

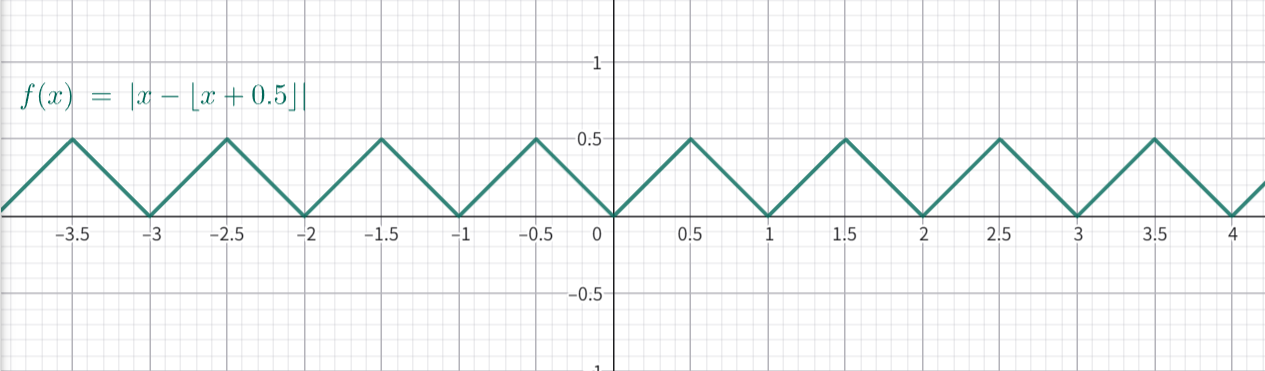
为了更直观的理解这个公式，可绘制函数 $y=\left|x-\left\lfloor{x}+0.5\right\rfloor\right|$ 的函数图像如下图所示：

从图中可以看到，这个函数是一个周期为1的一个锯齿状函数（后续简称为 $\text{grid}(x)$）。而其峰值为 0.5，当 $y=0$ 时为需要绘制 grid 的位置。

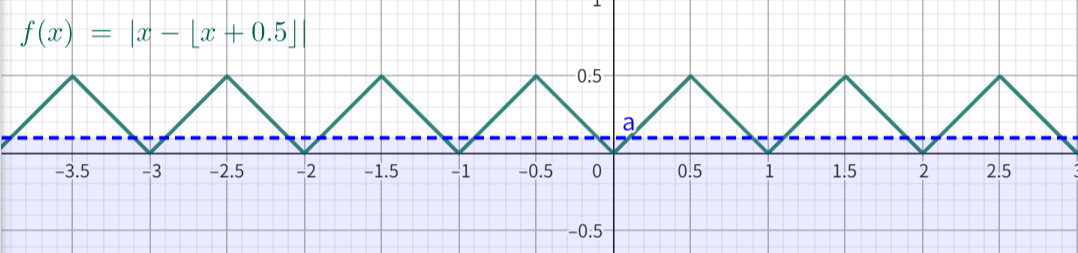
假设 $d=0.1$，我们实际需要绘制直线的区间就是下图中倒立的小三角形区域：

通过 $\text{grid}(x)$的函数图象不难观察发现，其几何意义就是 任意一点 $x$ 到其最近的整数（$0,1,\cdots$）的距离，这也是为什么 $d$ 可以用来控制网格线宽的原因（实际线宽为 $2d$）。

那么为什么在三维场景下线宽看上去并不统一呢？

在透视投影下，天然有近大远小的特性，距离相机越近，看上去越大。对于网格也是一样，如果我们在近处和远处都使用相同的线宽，就会出现线宽不一致的问题。

为了让我们在观测视角下看起来一直，就需要根据当前视角动态调整线宽，这就涉及到屏幕坐标系和世界坐标系下的尺度转换，也就是回答这么一个问题：

在世界坐标系下的某一个点绘制直线时，需要绘制多宽的直线才能在屏幕上看起来宽度是 2 个像素？

这一个可以通过屏幕空间的偏导数 $\frac{\partial f}{\partial u}$ 和 $\frac{\partial f}{\partial v}$ 进行计算，以世界坐标 $(x,y,z)$ 为例，设 $f(x,y,z) = (x,y,z)$，则 $\frac{\partial f}{\partial u}$ 和 $\frac{\partial f}{\partial v}$ 分别表示沿着屏幕空间 $u$ 方向变化一个像素时，世界坐标的变化情况。

而利用其倒数可以推导出，当世界坐标变化一个单位时，会在屏幕空间上变化多少个像素。

那么我们的目标函数 $\text{dist}$ 就可以转换成屏幕空间下的距离函数 $\text{dist}_{\text{s}}$ ： \[ \text{dist}_\text{s} = \frac{\text{dist}}{ \sqrt{ \left(\frac{\partial f}{\partial u}\right)^2 + \left(\frac{\partial f}{\partial v}\right)^2 } } \] 其中 $\sqrt{ \left(\frac{\partial f}{\partial u}\right)^2 + \left(\frac{\partial f}{\partial v}\right)^2 }$ 表示梯度 $ \grad f = \left(\frac{\partial f}{\partial u},\frac{\partial f}{\partial v}\right)$ 的 $L^2$ 范数（梯度向量在二维空间上的长度，可以理解为是在梯度方向上的变化率是多少）。

在实际计算过程中，可以差分方式进行近似，利用相邻像素之间的值计算，即 \[ \begin{align} \frac{\partial f}{\partial u} &\sim f(u+1,v) - f(u,v) \;\; \text{or} \;\; f(u,v) - f(u-1,v) \\ \frac{\partial f}{\partial v} &\sim f(u,v+1) - f(u,v) \;\; \text{or} \;\; f(u,v) - f(u,v-1) \end{align} \] 而 $\norm { \grad f}_2$ 可以通过 $\norm { \grad f } _1$ 进行近似： \[ \norm { \grad f}_2 \sim \abs{\frac{\partial f}{\partial u}} + \abs{\frac{\partial f}{\partial v}} \] 这三个值可分别在 shader 中使用 dFdx 、dFdy 和 fwidth 进行计算，利用 fwidth，就可以实现固定线宽的grid绘制，代码如下：

3d-grid-v2.frag

#version 330 core
in vec3 near_point;
in vec3 far_point;
out vec4 out_color;

uniform mat4 proj_view;
uniform float near;
uniform float far;

uniform vec3 grid_color = vec3(0.1,0.1,0.1);
uniform float grid_size = 0.5;
uniform float grid_thickness = 1.5;

vec4 draw_grid(vec3 world_pos, float grid_size, float grid_thickness, bool draw_axis){
  vec2 grid_coord = world_pos.xz / grid_size;
  vec2 grid_dist_world = abs(grid_coord - floor(grid_coord + 0.5));
  vec2 grid_dist_screen = grid_dist_world / fwidth(grid_coord);
  float draw = float(
    (abs(grid_dist_screen.x) < grid_thickness) ||
    (abs(grid_dist_screen.y) < grid_thickness)
  );
  return vec4(grid_color,draw);
}

void main() {
    float t = -near_point.y / (far_point.y - near_point.y);
    vec3 world_pos = near_point + t * (far_point - near_point);
    float draw_plane = float(t>0.0);
    vec4 color = draw_grid(world_pos,grid_size,grid_thickness,true);
    out_color = vec4(color.xyz,draw_plane * color.w);
}

绘制效果如下：

可以看到，此时线宽是固定了，但是远处的grid直接变成一片黑了，看起来效果非常差。

深度处理

为了更好呈现三维效果，我们需要确保网格可以被正常的遮挡，不然看起来就和平面一样。

这就需要我们可以正常的输出平面上的深度信息，只需要在交点处重新计算深度即可：

按照正常投影过程，经过 View Transform 和 Project Transform 得到 NDC 坐标，将深度信息设置到 gl_FragDepth 。

Tip

稍微需要注意的是，在 OpenGL 中，需要将 NDC 输出的深度范围是 $[0,1]$，即 z 轴坐标需要从 $[-1,1]$ 调整至 $[0,1]$

抗锯齿

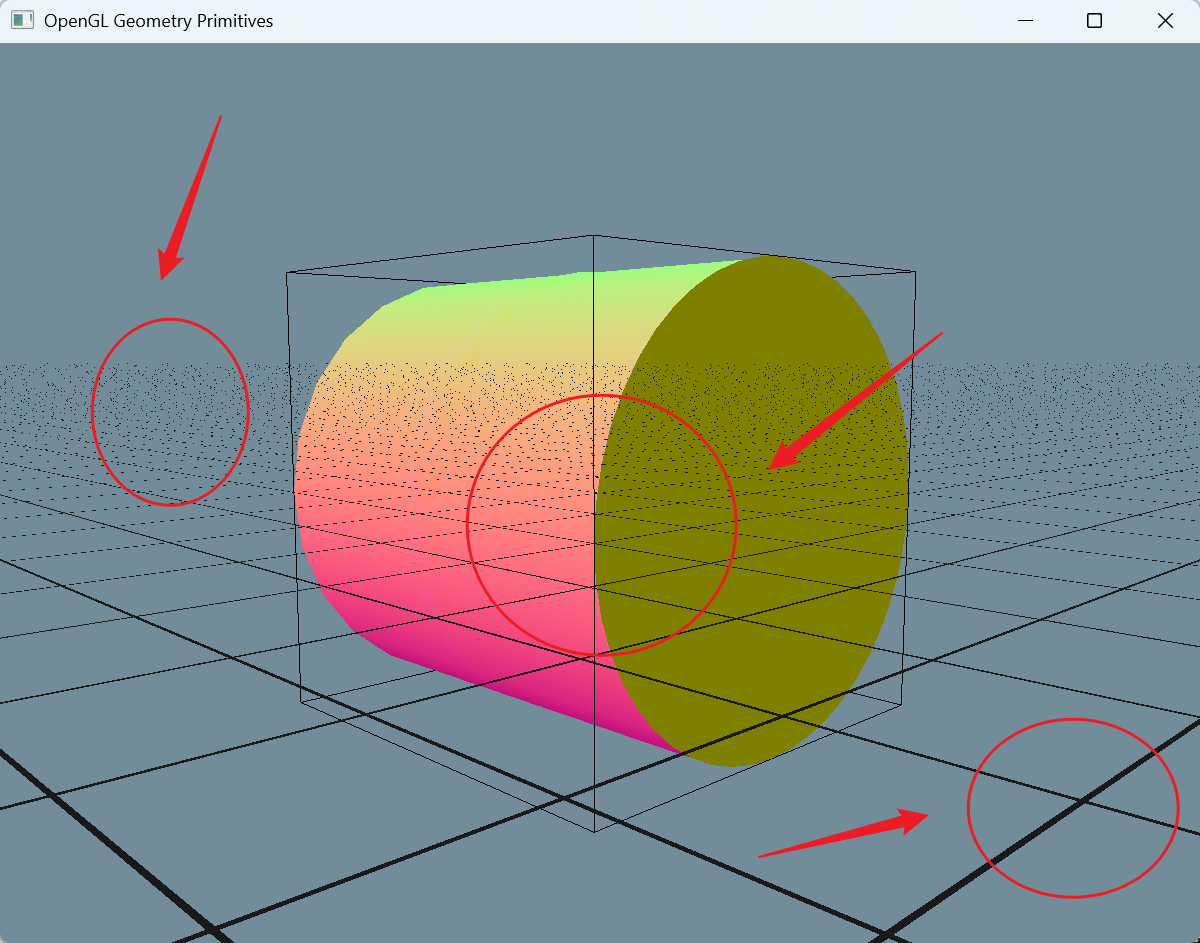
可以看到，在远处的 grid 中，出现了摩尔纹，局部放大图像时也可以看到锯齿状的图样

这是因为我们使用的是 clip 的方式进行绘制，只要 $\text{dist}_\text{s}$ 在指定宽度范围内，就会绘制整个像素。如果绘制区域仅覆盖了一个像素中的一部分，却将整个像素都绘制，就会出现锯齿（alias），在高频区域则会出现摩尔纹现象。

为实现抗锯齿，也就是需要估计网格在绘制边界的像素覆盖率，当网格边界仅覆盖一部分像素时，将返回的颜色（或alpha值）设置为实际覆盖的比例。

覆盖率计算如下图所示，在当前像素（红色方块）计算的距离为 2.7，由于此时使用的是像素中心点进行计算，实际像素的范围是$(2.2,3.2)$

再结合网格线宽为 6 ，可以计算该像素的覆盖率为 $6 * 0.5 - 2.7 + 0.5 = 0.8$

此处多加的 0.5 是像素本身被覆盖的部分。

将覆盖率的计算公式一般化，如下式所示： \[ \text{cov} = \left(\frac{l}{2} -\text{dist}_{\text{s}} \right) + 0.5 \\ \] 当 cov 大于 1时，说明像素一定被完全覆盖，当 cov 小于1时，说明像素一定不会被覆盖。

那么可以加上一个 clamp 以确保结果范围，由于我们的 grid 包含两个方向，取 cov 最大的一个方向作为最终 cov 的估计值，可以写出添加上抗锯齿实现后的 shader 代码

3d-grid-v4.frag

#version 330 core
in vec3 near_point;
in vec3 far_point;
out vec4 out_color;

uniform mat4 proj_view;
uniform float near;
uniform float far;

uniform vec3 grid_color = vec3(0.1,0.1,0.1);
uniform float grid_size = 0.5;
uniform float grid_thickness = 2.0;
uniform float max_depth = 0.5;
uniform float set_depth = 0.0;

float compute_depth(vec3 pos) {
    vec4 clip_space_pos = proj_view * vec4(pos.xyz, 1.0);
    // re-arrange depth to 0~1
    return (clip_space_pos.z / clip_space_pos.w) * 0.5 + 0.5;
}

float compute_linear_depth01(float zndc) {
  float z01 = (2.0 * near) / (near + far - (far - near) * zndc);
  return z01;
}

vec4 draw_grid(vec3 world_pos, float grid_size, float grid_thickness, bool draw_axis){
  vec2 grid_coord = world_pos.xz / grid_size;
  vec2 grid_dist_world = abs(grid_coord - floor(grid_coord + 0.5));
  vec2 grid_dist_screen = grid_dist_world / fwidth(grid_coord);
  vec2 cov = clamp((grid_thickness * 0.5 - grid_dist_screen) + 0.5,0.0,1.0);
  float draw4 = max(cov.x,cov.y);
  return vec4(grid_color,draw4);
}

void main() {
    float t = -near_point.y / (far_point.y - near_point.y);
    vec3 world_pos = near_point + t * (far_point - near_point);
    float depth = compute_depth(world_pos);
    gl_FragDepth = set_depth * depth;
    float depth01 = compute_linear_depth01(depth * 2.0 - 1.0);
    float draw_depth = mix(max_depth,0.0,depth01);
    float draw_plane = float(t>0.0);
    vec4 color = draw_grid(world_pos,grid_size,grid_thickness,true);
    out_color = vec4(color.xyz,draw_depth * draw_plane * color.w);
}

对比没开启抗锯齿之前的绘制效果如下

细节处理

到此为止，我们绘制的 grid 已经算基本可以看了，对比 blender 中的网格，还剩最后3个细节：

在 x = 0 和 y = 0 处的grid颜色有区别
每个大 grid 中包含若干小 grid，且大 grid 的线宽更宽
远处的 grid 会渐渐的消失（区别于前面提到的depth fading）

为实现第一个效果，我们需要在绘制中判断当前绘制的直线是否在特殊网格线上。以 $x=0$ 为例，只要判断当前世界坐标是否在 $x=0$ 的绘制范围即可，如下所示： \[ \begin{align} \frac{\abs{x}}{w} &< \frac{l}{2} \\ \abs{x} &< \frac{l}{2} \cdot w \end{align} \] 其中 $w$ 就是之前利用 fwidth 计算得到的一个像素对应 grid 的长度，$l$ 为线宽（单位为像素）

对于第二个效果，我们只需要使用不同分辨率的 grid 绘制变量，然后将结果通过 alpha 混合即可。

对于第三个效果，是为了解决远处的 grid 糊在一块的问题。对于远处的 grid，其大小非常小，导致一个像素会覆盖多个 grid 直线。为此，我们可以在绘制时判断 grid 在屏幕空间的大小，如果 grid 太小（例如小于 1 px），就直接不绘制即可（也可以通过 smoothstep 实现光滑的过度）。

最终完整代码如下：

3d-grid-v5.frag

#version 330 core
in vec3 near_point;
in vec3 far_point;
out vec4 out_color;

uniform mat4 proj_view;
uniform float near;
uniform float far;

uniform vec3 grid_color = vec3(0.1,0.1,0.1);
uniform float grid_size = 0.5;
uniform float minor_grid_scale = 5;
uniform float grid_fade_size = 5.0;
uniform float grid_thickness = 2.0;
uniform float max_depth = 0.5;

float compute_depth(vec3 pos) {
    vec4 clip_space_pos = proj_view * vec4(pos.xyz, 1.0);
    // re-arrange depth to 0~1
    return (clip_space_pos.z / clip_space_pos.w) * 0.5 + 0.5;
}

float compute_linear_depth01(float zndc) {
  float z01 = (2.0 * near) / (near + far - (far - near) * zndc);
  return z01;
}

vec4 draw_grid(vec3 world_pos, float grid_size, float grid_thickness, float fade_size){
  vec2 grid_coord = world_pos.xz / grid_size;
  vec2 grid_dist_world = abs(grid_coord - floor(grid_coord + 0.5));
  vec2 grid_size_scaler = fwidth(grid_coord);
  // grid size in screen space
  vec2 grid_size_pixel = 1.0 / grid_size_scaler;
  float min_spacing = min(grid_size_pixel.x,grid_size_pixel.y);
  float size_fade = smoothstep(0.0,fade_size,min_spacing);
  vec2 grid_dist_screen = grid_dist_world * grid_size_pixel;
  float half_grid_thickness = 0.5 * grid_thickness;
  vec2 cov = clamp((half_grid_thickness - grid_dist_screen) + 0.5,0.0,1.0);
  float draw = max(cov.x,cov.y);
  float x_axis = float(abs(grid_coord.x) < half_grid_thickness * grid_size_scaler.x);
  float z_axis = float(abs(grid_coord.y) < half_grid_thickness * grid_size_scaler.y);
  vec3 color = x_axis * (1.0 - z_axis) * vec3(1.0,0.0,0.0) + 
               z_axis * (1.0 - x_axis) * vec3(0.0,0.0,1.0) + 
               step(x_axis + z_axis,0.5) * grid_color;
  return vec4(color, draw * size_fade);
}

vec4 alpha_blend(vec4 fg, vec4 bg) {
  return vec4(
    fg.rgb * fg.a + bg.rgb * (1.0 - fg.a),
    fg.a + bg.a * (1.0 - fg.a)
  );
}

void main() {
    float t = -near_point.y / (far_point.y - near_point.y);
    vec3 world_pos = near_point + t * (far_point - near_point);
    float depth = compute_depth(world_pos);
    float linear_depth = compute_linear_depth01(depth * 2.0 - 1.0);
    gl_FragDepth = depth;
    float draw_depth = mix(1.0,0.0,max(linear_depth,max_depth));
    float draw_plane = float(t>0.0);
    // minor grid
    vec4 color1 = draw_grid(
        world_pos,grid_size, grid_thickness * 0.5, grid_fade_size);
    // major grid
    vec4 color2 = draw_grid(
        world_pos,grid_size * minor_grid_scale, 
        grid_thickness, grid_fade_size * minor_grid_scale);
    // alpha blend two color (color1 is base, and color2 is foreground)
    vec4 color = alpha_blend(color2, color1);
    out_color = vec4(
      color.rgb,
      draw_depth * draw_plane * color.a
    );
}

最后给一个完整的效果