投影变换矩阵
Hello Projection
所谓投影,就是 将高维空间中的对象,通过某种方式映射到低维或另外一个空间中。如下图所示(图片来自网络)。
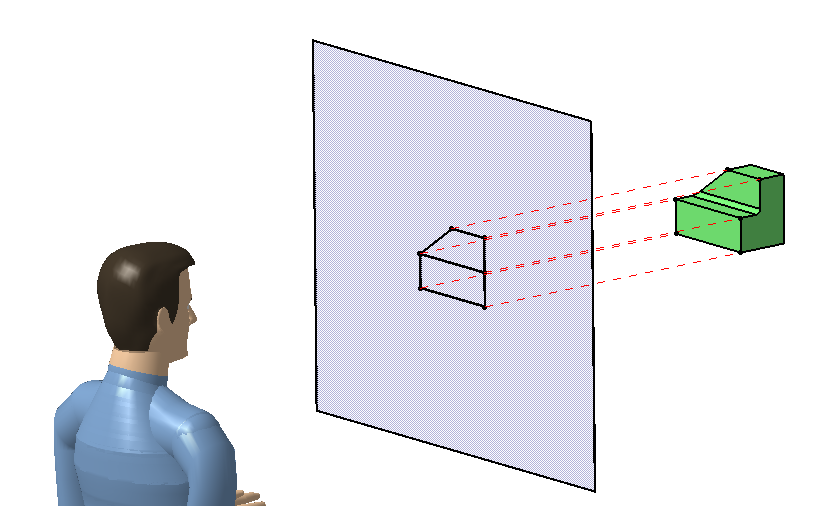
当在二维平面上展示三维物体时,其展示的是三维物体在二维空间上的一个投影,而这个三维到二维的转换过程就是投影变换。
如果投影过程是一个线性变换,则可以通过一个矩阵描述变换,如下式所示,其中 \(M_\text{projection}\) 就称为投影变换矩阵。 \[ P^{\prime} = M_{\text{projection}} \cdot P \]
正交投影
正交投影的一个特点就是不会改变线之间的平行关系,因此待投影的区域一定会是一个长方体,可以通过六个坐标信息 (l,r,t,b,n,f) 来代表这个长方体,分别代表 左,右,上,下,前,后 面的坐标(left,right,top,bottom,near,far) 。
满足(l<r,b<t,f<n,此处f小于n是因为我们从z轴的负向看去)。
投影目标是将其将这个长方体中心移动至原点并转换成单位正方体(也称为 NDC,normalized device coordinate)。
那么实际的正交投影矩阵就可由两个变换构成,平移变换和缩放变换。
单位正方体坐标为 (l,b,n) = (-1,-1,-1) ,(r,t,f) = (1,1,1),此处n坐标就小于f坐标,符合我们正常的认知(从z轴正向看去,离得越远z坐标越大)
而实际待投影的长方体的长宽高和中心如下 \[ \begin{align*} &(r-l,t-b,n-f) \\ &(\frac{r+l}{2},\frac{t+b}{2},\frac{n+f}{2}) \end{align*} \] 因此我们首先将其中心移动至(0,0,0),对应的转移矩阵为 \[ T(\hat{t}) = \left[ \begin{matrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{matrix} \right] \] 然后将长方体转换成标准正方体即可(正方体的边长为2) \[ S(\hat{s}) = \left[ \begin{matrix} \frac{r-l}{2} & 0 & 0 & 0 \\ 0 & \frac{t-b}{2} & 0 & 0 \\ 0 & 0 & \frac{n-f}{2} & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \] 经过这两步之后实际上得到的单位正方体的前后坐标还是n大于f(n=1,f=-1),不太符合日常认知,可以对其z坐标做一个镜像将其转换成 n = -1,f = 1,只需要在z轴上取反即可 \[ M_z= \left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \] 最终组合这三个操作,就可以得到最终的正交投影矩阵 \[ \begin{align*} P_O = M_zS(\hat{s})T(\hat{t}) & = \left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{matrix} \right] \\ & = \left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{f-n} & -\frac{n+f}{f-n} \\ 0 & 0 & 0 & 1 \end{matrix} \right] \end{align*} \]
上面写的稍微有点繁琐,因为 \(n\) 和 \(f\) 默认假设视角从原点看向 z 轴负向,坐标值都是小于 0 ,有 \(f<n\)。为保证长宽高的大小为正值,就会有 \(n-f\) 为缩放长度。
实际上要确保 \(n\) 在 ndc 下的 \(z=-1\) 处,\(f\) 在 ndc 下的 \(z = 1\) 处,直接使用 \(f-n\) 即可,其几何意义就是将 \([n,f]\) 区间直接缩放到 \([-1,1]\)区间,二者是一样的,只不过这样一步到位隐含了一个方向反转的过程。
透视投影
和正交投影相比,透视投影满足近大远小的效果,平行的线在透视投影中将不再平行,会相交于一点,能体现出深度变化情况,让人看起来更有立体感。
因此,我们待投影的区域不再是一个长方体,而是一个平台锥(frustum,又称为视锥体),为了将这个锥体投影到2维平面中,我们首先需要将视锥体转换成长方体,之后再按照正交投影即可。
下面展示了视锥体的示意图:
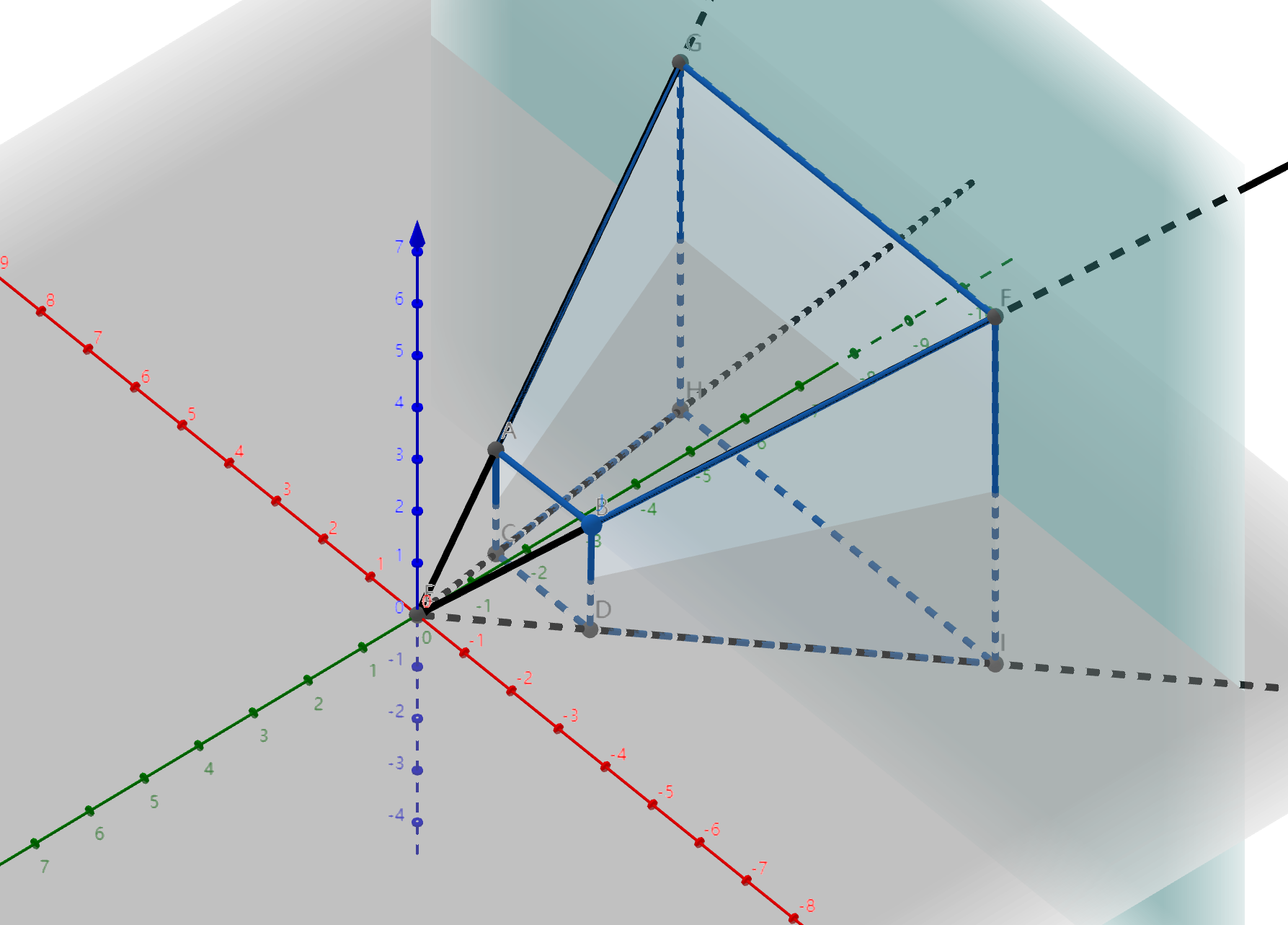
简单推导一下如何将视锥体转换成长方体,从图中可以观察到3个性质:
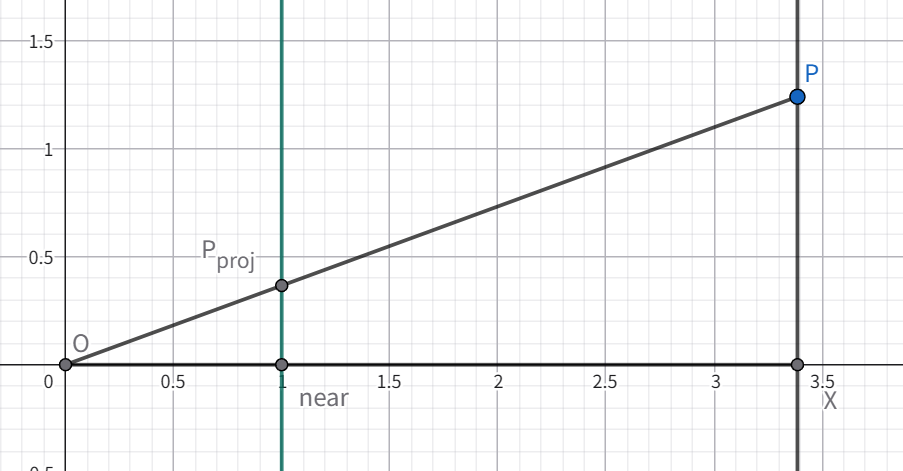
锥体中任意一点在n面上的投影为过原点和该点的连线同n面的交点,满足相似三角形性质,如下图所示:
![]()
锥体的前面(n面,对应投影面)上的点坐标并不发生变化
锥体的后面(f面)中心位置不会变化,即\((0,0,f)\)投影后应该还是 \((0,0,f)\)
首先根据观察1:相似三角形,满足如下公式 \[ \begin{align*} \frac{x}{z} = \frac{x_{\text{proj}}}{n} & \quad x_{\text{proj}} = \frac{n}{z} \cdot x \\ \frac{y}{z} = \frac{y_{\text{proj}}}{n} & \quad y_{\text{proj}} = \frac{n}{z} \cdot y\\ \end{align*} \] 可以得出投影区域内任意一点 \((x,y,z,1)\) 在 n面上的投影为 \((\frac{n}{z}x,\frac{n}{z}y,?,1)\),同时乘上 \(z\) 写成 \((nx,ny,?,z)\) ,此处投影后的 \(z\) 值未知是因为投影到二维 \(xy\) 平面上只需要\(x\) 和 \(y\) 即可,其 \(z\) 值具体是多少还不知到,可以先写出转换矩阵的第1、2、4行: \[ M_\text{perspective} = \left[ \begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ A & B & C & D \\ 0 & 0 & 1 & 0 \end{matrix} \right] \] 接下来就只剩下矩阵的第三行,使用前两个特点可以得出第三行取值:
由观察2:n面上任意一点的坐标不会变化,因此有 \[ \begin{align*} P_1^{\prime} & = (x,y,n,1) \\ & = M_\text{perspective} P_1 \\ & = (nx,ny,Ax+By+Cn+D,n) \\ & = (nx,ny,n^2,n) \end{align*} \] 可得出等式 \[ Ax + By + Cn + D = n^2 \] 又由于该等式对投影区域内任意一点都成立,因此A和B一定为0 \[ \begin{cases} A = 0 \\ B = 0 \\ Cn + D = n^2 \end{cases} \] 再由观察3:f面中心坐标不变,则有 \[ \begin{align*} P_2^{\prime} & = (0,0,f,1) \\ & = M_\text{perspective}P_2 \\ & = (0,0,Cf+D,f)\\ & = (0,0,f^2,f) \end{align*} \] 即 \[ Cf + D = f^2 \] 联立两式可得 \[ \begin{cases} Cn+D = n^2 \\ Cf+D = f^2 \end{cases} \] 可得A和B如下 \[ \left\{ \begin{array}{ll} C = n+f\\ D = -nf \end{array} \right. \] 则可得完整的透视转换矩阵为 \[ \left[ \begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{matrix} \right] \] 经过转换之后,待投影区域已经变成一个长方体了,此时我们只需要使用正交投影将其转换为标准立方体即可 \[ P_P = P_OM_\text{perspective} = \left[ \begin{matrix} \frac{2n}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2n}{t-b} & 0 & 0 \\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & 1 & 0 \end{matrix} \right] \]
此时矩阵的参数还有点多(6个),我们可以默认带投影区域是关于 \(z\) 轴对称的,且观测点在原点,这样 \(r-l\) 和 \(t-b\) 就可以通过 aspect 和 fov 两个参数代替: \[ \begin{align} \text{w} & = r - l \\ \text{h} & = t - b \\ \text{aspect} & = \frac{\text{w}}{\text{h}} = \frac{r-l}{t-b} \\ \text{fov} & = 2 \arctan (\frac{\text{h}}{n}) \\ c &= \frac{2n}{t-b} = \frac{1}{\tan(\frac{\text{fov}}{2})} \\ a &= \text{aspect} \end{align} \] 这样,只需要 aspect,fov,near,far四个参数就可以得到最终的变换矩阵:
\[ P_P = P_OM_\text{perspective} = \left[ \begin{matrix} \frac{c}{a} & 0 & 0 & 0 \\ 0 & c & 0 & 0 \\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & 1 & 0 \end{matrix} \right] \]
通过矩阵计算后得到的是齐次坐标,执行透视除法得到投影后的三维NDC坐标: \[ \begin{pmatrix} x_\text{ndc}\\ y_\text{ndc}\\ z_\text{ndc} \end{pmatrix}= \begin{pmatrix} {\tfrac {x_{c}}{w_{c}}}\\ {\tfrac {y_{c}}{w_{c}}}\\ {\tfrac {z_{c}}{w_{c}}} \end{pmatrix} \]
此时 \(z_\text{ndc}\) 的取值范围为 \([-1,1]\),(原始 z 的取值范围为 \([n,f]\) ),如果需要变成 z-buffer 中实际存储的值,还需要进行一次线性变换(一般会自动在 viewport 变换中执行),将 \([-1,1]\) 区间转换到 \([0,1]\) 的区间内,变成 z-buffer 中实际存储的值,如下式所示: \[ z_{\text{buffer}} = 0.5 * (z_{\text{ndc}} + 1) \]
深度转换
在shader中常需要进行 \(z_{\text{ndc}}\) 和原始坐标 \(z\) 的转换,可以根据上面矩阵公式计算出其关系: \[ \begin{align} z_\text{ndc} & = \left(\frac{f+n}{f-n} \cdot z - \frac{2nf}{f-n}\right) \cdot \frac{1}{z} \\ & = \frac{f+n}{f-n} - \frac{2nf}{(f-n) \cdot z} \\ z & = \frac{2nf}{f+n - (f-n)\cdot z_\text{ndc}} \end{align} \]
如果需要获得归一化的的线性深度,那么还需要将 \(z\) 标准化到 \([0,1]\) 区间内,即 \[ z_{\text{depth01}} = \frac{z-n}{f-n} \] 在实际情况下 n是一个很小的值,基本可以忽略不计,因此可以简化为 \(\tilde{z}_{\text{depth01}} = z / f\) ,这样我们计算公式可以简化为 \[ \tilde{z}_\text{depth01} = \frac{2n}{f+n-(f-n) \cdot z_{ndc}} \] 根据 \(z_{\text{buffer}}\) 、\(z_\text{depth01}\) 和 \(z\) 之间的关系,可以绘制如下曲线(\(n=1\),\(f=10\))

其中:
- 灰色曲线代表 \(z_\text{buffer}\)
- 绿色直线代表 \(z_{\text{depth01}}\)
- 蓝色和红色竖线代表 \(n\) 和 \(f\)
- \(x\) 轴对应原始的 \(z\)
从图中可以看出,\(z\) 是线性增加的, 而 \(z_\text{ndc}\) 并不是,而是随着 \(z\) 的拉大,深度之间的差异越来越小。这也符合近大远小的要求(越近的物体对深度的精度要求更高)。
当我们需要进行深度比例的计算时,就需要使用线性深度值,此时可以将 \(z_\text{ndc}\) 转换为 \(z_\text{depth01}\) 后进行后续计算。