空间填充曲线

对于一个\(2^n\times2^n\)的二维网格由于地址空间都是一维的（例如0x0000到0xffff），其实际在计算机中会将多维压缩成一维，可以形式化表示为

\[ \begin{align} M_{\text{2D}}&:(x,y)\to v \\ M_{\text{2D}}^{-1}&:v\to (x,y) \\ \end{align} \]

对于\(M_{\text{2D}}(x,y)\)也可记作\(\text{encode}(x,y)\)，\(M^{-1}_{\text{2D}}(v)\)为\(decode(v)\)

Linear Curve

一种最为简单的存储方式就是逐行地或逐列地存储二维数据，对于一个指定大小的二维方块（\(w\times h\)），从0开始的坐标\((x,y)\) 对应的一维地址为（一行包含\(w\)个元素） \[ v = x \times w + y \] 同理，将一维坐标\((v)\)转换二维方块坐标也很简单，只需要对行/列进行整除和取余操作即可 \[ \begin{align} x &= \lfloor v / w \rfloor \\ y &= v - x \times w \end{align} \] 上面这种方式在一般情况下足够使用，但是对于纹理/体素等数据的读取时，通常会利用到二维/三维坐标的局部性（即当我们访问坐标\((x,y)\)时，我们有很大概率将访问该坐标周围的坐标），而使用线性存储方式则会丢失这种局部性。

例如对于一个\(16 \times 16\)的方块中坐标\((4,4)\)和坐标\((6,6)\)，其二维曼哈顿距离为 \[ (6-4)+(6-4) = 4 \] 而经过线性存储映射后距离为 \[ (6*16+6)-(4*16+4)=38 \] ，可以观察到经过一维映射后两个数据距离相差较远。

下图展示了 linear curve 的示意图

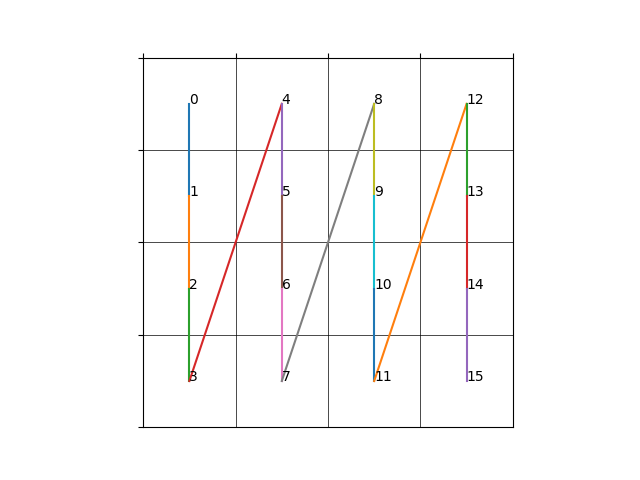
直接说距离似乎难以理解这种差距，考虑一个实际读取场景，假设CPU的cache一次可以存放16个数据，当我们读取纹理中\((4,4)\)位置的数据后，下一个准备读取其周围\((6,6)\)的数据，由于\((6,6)\)的数据在内存中地址距离\((4,4)\)数据地址较远，无法一次加载到cache中，即出现cache miss，这样我们就只能从内存中重新加载数据，无法利用高速缓存，影响数据读取性能。

针对这个问题，可以使用Hilbert曲线或者Morton曲线这类特殊的映射方式进行坐标映射

Hilbert Curve

每一个\(2^n \times 2^n\)的方块，都可以对应一个\(n\)阶的曲线，下图给出了1阶Hilbert Curve曲线的示意图

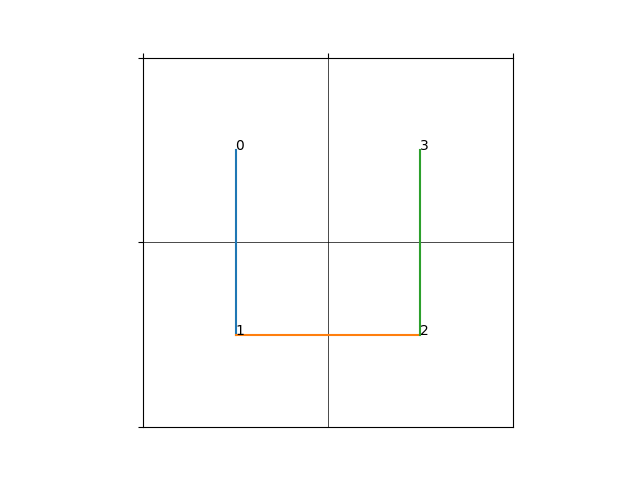
对于\(2\times2\)的方块（x轴向左，y轴向下），曲线是一个U字形，二维坐标顺序为： \[ (0,0) \to (0,1) \to (1,1) \to (1,0) \] 对应的一维坐标顺序（二进制形式）为： \[ 00_2\to01_2\to10_2\to11_2 \]

下面给出2阶Hilbert Curve曲线示意图

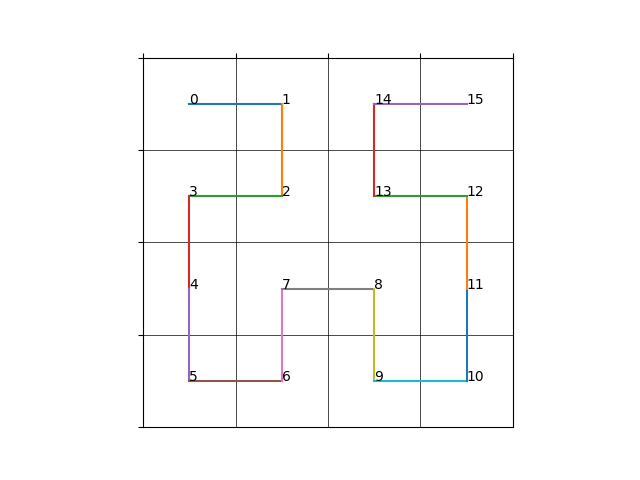
对于\(4\times4\)的方块，将其转换为4个\(2\times 2\)的小方块，然后观察每一个小方块的形状和朝向，会发现这几个小方块的形状完全一致（都是U型），只是朝向不同。块与块之间会额外添加直线连接，同样可以写出二维坐标和一维坐标的映射：

二维坐标 \[ \begin{align} (0,0)\to(1,0)\to(1,1)\to(0,1)\\ \to(0,2)\to(0,3)\to(1,3)\to(1,2)\\ \to(2,2)\to(2,3)\to(3,3)\to(3,2)\\ \to(3,1)\to(2,1)\to(2,0)\to(3,0) \end{align} \] 一维坐标 \[ \begin{align} 0000_2\to0001_2\to0010_2\to0011_2\\ \to0100_2\to0101_2\to0110_2\to0111_2\\ \to1000_2\to1001_2\to1010_2\to1011_2\\ \to1100_2\to1101_2\to1110_2\to1111_2\\ \end{align} \] 从二维坐标中可以发现，每一个\(2 \times 2\)子方块都是一组，可以写出四个方块的中心： \[ (0,0) \to (0,2) \to (2,2) \to (2,0) \] 此处可以观察到，四个子方块的中心实际上就是一阶Hilbert曲线的放大两倍的结果

然后将每个子方块的坐标减去方块中心，可以得到如下四组坐标： \[ \begin{align} (0,0)\to(1,0)\to(1,1)\to(0,1)\\ (0,0)\to(0,1)\to(1,1)\to(1,0)\\ (0,0)\to(0,1)\to(1,1)\to(1,0)\\ (1,1)\to(0,1)\to(0,0)\to(1,0) \end{align} \] 其中第1组和第4组的分别是一阶Hilbert曲线沿\(y=x\)和\(y=1-x\)直线翻转的结果，为便于表示，使用\(F\)和\(FR\)表示（\(FR\)表示沿\(y=x\)翻转后再旋转\(180\degree\)，由此可得二阶Hilbert曲线构造过程：

$$

$$

下面给出3阶Hilbert Curve曲线示意图

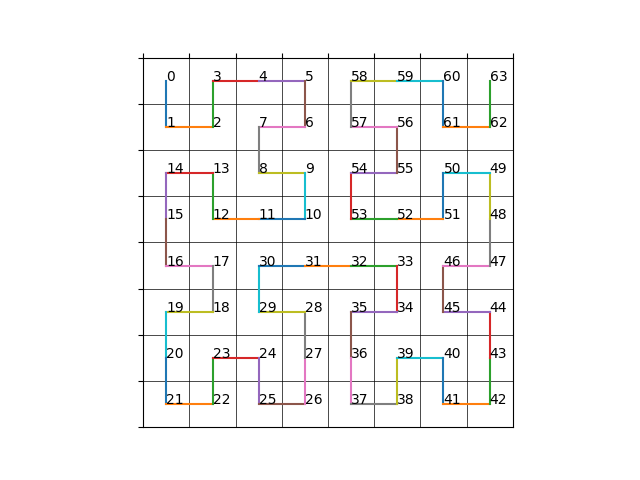
根据1、2和3阶的Hilbert Curve示意图，我们已经可以大概看出规律，对于每一个\(2^n\times 2^n\)的方块，其下一层（即4个\(2^{n-1}{\times}2^{n-1}\)块）也是Hilbert Curve，其存在自相似性。

Morton Z Curve

后记

对于三维或者更高维度的数据存储，都可以采用Hilbert或者Morton方式进行存储，映射方式同二维映射类似（稍微复杂一点），这样在访问中存在空间局部性的应用较为友好，可以提高数据读写的性能。